[ML] Adaboost part 1
當年我第一個學的ML algorithm, 就是Adaboost (Adaptive boosting)
Adaboost wiki: http://en.wikipedia.org/wiki/AdaBoost
因為他在平均辨識偵測的表現上, 算是較好的, 參數不多效果好, 好learning, 不學嗎?
其實應該是說這比SVM好介紹...所以Adaboost先登場XD
不過, 通常Adaboost要登場前, 要先拿Bagging拿出來鞭
一種ML演算法, 後來大多指sampling的方法, 這種演算法很簡單
我們手上有input, 我用一個classifier去學習他, 可是如果data太複雜怎辦?
所以乾脆這樣, 我用多個classifier來學這些data, 可是如果data都一樣, 那學完的結果還是一樣
所以呢, 乾脆取樣部份sample就好, 就用一招select with replacement來取樣
意思就是, 假設我有N筆data, 我取N筆, 但是每取一筆, 我就會放回, 最後得到的N', N' <= N
也就是可能會有重複的, 但是最後同一筆只算一次, 那數量就會比原本的N少
每個classifier所需要的data都做這種事情, 最後就會有T種classifier, 判斷也很簡單, 就叫這些classifier投票, 獲選可能的class最多的為主 (majority vote)
不過可惜的是,沒啥理論依據證明這夠好(根據我教授來信指出: 其實是有理論的, 但因為沒有太多的實務上的成果說明他夠好, 所以就比較少人使用!!), 而且bias會影響這種方式, 所以就有人發明了boosting方法!!
最早由Yoav Freund 和 Robert Schapire一起在1996年提出(所以這是一個有17年以上的演算法....)
原文: http://www.face-rec.org/algorithms/Boosting-Ensemble/decision-theoretic_generalization.pdf
不想看原文沒關係, 由我來打打嘴泡XD (打完的感想...我根本自虐嘛!!!)
既然原名是Adaptive boosting, 就先從boosting開始講起
假設我今天有100筆資料要給電腦學習, 你手上需要寫一個演算法要去判斷這些資料, 所以去找了paper看ML演算法來判斷
結果因為厲害的演算法太複雜了或者是paper太難了看不懂, 只寫出了很笨很簡單的演算法(weak learner), 效果又不是那麼的好, 那怎麼辦呢?
那就用boosting吧!!, boosting可以加強你的笨笨演算法, 可以不停的演化修正錯誤達到高水準分類器!!
聽起來超威的耶, 那boosting要如何使出來呢? (絕對不是上上下下左左右右ABAB)
boosting的基本idea是這樣的, 你手上的演算法判斷了data之後, 每筆data都會有所謂的錯誤率, 透過修正這些錯誤率, 來強化原本的weak learner
也就是說, 假設每個training data都有個錯誤權重, 一開始大家都一樣, 因為還沒判斷, 等到weak learner開始判斷之後, 每個data都有自己的錯誤率, 把猜錯的提高權重, 猜對的降低權重, 如此一直循環下去, 就會慢慢的提昇learner的能力
PS1: 所以不能選太強的learner, 因為不容易加強
PS2: 所以learner要選可以餵入weight的
假設每個training data都有初始weight, D (distribution), 大家一開始都一樣, 當weak learner A學完第一輪之後, 判定大家的結果, 然後調整weight, 再用weak learner B去重新學調整過後的D, 然後weak learner C...etc
最後再統合(Ensemble)這些weak learner的結果, 來達到一個strong learner
那上述是簡易描述, 再來是眾多的定義
0. Weak learner, 稍微給點簡單定義, 以猜測正反來講, 隨機猜中的機率是0.5, 那weak learner大概就是比0.5再高的那麼一點點罷了, 這個內容會再另外交代
1. Input: 假設有N筆資料, x是feature的意思, y是所屬class, 通常paper會寫成 sequence of N labeled examples <(x1, y1), ..., (xN, yN)>, 那我們先著重在Binary的分類, 所以y基本上不是1 就是 -1 (是否之類的問題, 當然也可以是1 or 0, 到證明的時候會比較計較)
2. Iteration: 每次重新學習會是一個循環, 假設總共會重新學習 T 回, 每小回簡稱第t回
3. weight: 在這邊意思可以想成為distribution, 因為一開始大家都一樣, 所以一個簡單的預設初值可以這樣設定, D通常稱呼為 - distribution D over the N examples
t 就是上述的Iteration, D1的意思就是說第一回每個example的Distribution
4. 那再來就是用數學表示weak learner的結果, 首先每個learner 或者稱classifier, 都會學習一定的內容, 他會針對學習到的東西給一個假設, 例如說, 有一批人類的樣本學習, 然後他學到說假設眼睛有兩個以下的是人類, 這就是一個假設(hypothesis), 那來給點數學式
ht 意思就是第 t 回的weak learner, 那給定一個X vector, 會回傳1 or -1, X vector可以想成就是一筆眾多的features
5. error: 算錯誤率囉, 這應該很簡單, 把判斷錯的除以全部的數量, 就是錯誤率囉, trivial!!
6. 更新方法: 也就是前面說的, 有些權重要增加或減少, 更新的公式如下
下一回的權重怎麼更新呢? 就是把當回(t)的權重 Dt 乘上神妙的 e-αt or eαt 再除以原本的總和即可, 這取決於有沒有猜對, 有猜對就下降, 有猜錯就上升. 那Zt 意思是全體每個distribution還要再做normalization, 也就是全部加起來再除掉.
至於那個α為甚麼會是那樣, 放到最後解釋
7. 合併: 那我們手上有了每個回合的weak learner, 要怎麼合併呢? 統統拿去做雞精!! 喔不是, 是統統加起來!!
取sign的意思就是, 大於0我就認為是1, 小於0我就認為是-1, that's all.
以偷懶的角度, 我可以說我已經解釋完整個Adaboost了...那這樣跟自己去看wiki根本沒差阿XDD
所以有些事情要交代一下, 那個α哪來的, 以及這樣的classifier真的有比較好嗎?
classifier好不好要看錯誤率, 錯誤率要能夠降的夠低才行
那想要降低錯誤率, 就要找出影響錯誤率的因子是哪些, 下面就會開始找出關鍵的因子!!
先來看一下distribution, 這邊有個比較tricky的部份, 為了推導方便, 需要把真實的class跟classifier的猜測做比較這件事情合併進入公式
如果猜對的話, 不管class是1 or -1, yi乘上ht(xi)都會是1, 反之, 都會是-1, 所以可以改寫為
也就是不對的時候負號會抵銷掉, 對的時候會留著, 跟原本的設定一樣
再來辛苦一點, 把他展開來觀察
好像沒什麼, 這時候做一件證明很常做的事情, 左邊全部乘起來, 右邊全部乘起來
當然在衝動把他寫下來之前, 會發現左右有項次可以互相消除, 消完之後整理就會變成
看起來很簡單吧, 只是把exp裡面的全部加總起來, 下面的Zt只是全部乘起來, 這邊有沒有發現很眼熟的東西? 有沒有發現前面最後的H(x)居然在這裡出現了, 就是那個summation, 所以稍微替換一下
你會說, 奇怪, 替換了之後怎麼D1(i)怎麼不見了, 變成了1/N, 因為最一開始有假設, 第一回大家都是一樣的權重, 也就是1/N, 所以在這步我就順便替換了
再來稍微複雜一點點, 稍微來到Exponential的特性, Exponential的次方, 只要超過0, 都大於等於1
Exponential wiki: http://en.wikipedia.org/wiki/Exponential_function
那現在要來認真算錯誤率了, 假設, H(xi)犯錯的話, 會犯多少錯誤?
可以用數學表示大概會是怎樣的範圍嗎? 可以的, 但是要繞一點圈
假設H(xi)犯錯了, yi f(xi)會小於等於 0 (因為其中一個為1, 另外一個為-1), 那相乘的話一定小於0
所以配合exponential可以得到
我使用的工具不好打boolean operatior, 我改用indicator function表示, 也就是成立為1, 不成立為0
剛剛推完的Dt+1跟這邊好像很像, 我們把他合併來看一下
最後的步驟好像Dt+1不見了, 因為他是distribution, 最後全部加起來當然會是1, 所以一乘上去, 就消失囉
這裡告訴我們甚麼? 就是想要把錯誤率降低的話, 降低Zt 就可以了, 這邊可以想成是他的error upper bound
那這跟α甚麼關係呢? 其實事情是這樣的, 我上面只是找到了說, 如果今天會犯錯, 犯錯的錯誤率最大會被bound在Zt, 那所以只要想辦法把Zt弄小的話, 整個錯誤率就會下降對吧!!
那, 回到微積分, 所以只要我們對Zt做偏微 = 0, 就可以判斷出極值, 也就找到了可以下降的關鍵!! (並非所有演算法都可以這樣解, 只是這個剛好可以求出解來)
可以分出兩種狀況, 有猜對跟猜錯的, 所以可以改寫成下列結果
中間有把錯誤率ε替換一下, 意思就是, 我將可能分成兩種, 猜對跟猜錯, 然後替換一下
這邊過來那邊過去, 兩邊取ln, 就解出來了, 這就是α最美好的狀態, 可以讓錯誤率達到最低
基本上學到這邊該會的應該都會了, 剩餘的就是實做了!!
實做部分跟weak learner留到下一篇~!!
(以前我教授教我的Adaboost其實還有很多很難的東西, 大多是證明...但是我快忘光了XD, 等我想起來再補上, 這邊只是參考原作者的論文跟網路上比較常見的證明而已)
PS: 我用過而且算是好用的Adaboost tool有: 1. Weka 2.我教授他同窗的好友做的Lemga
Adaboost wiki: http://en.wikipedia.org/wiki/AdaBoost
因為他在平均辨識偵測的表現上, 算是較好的, 參數不多效果好, 好learning, 不學嗎?
其實應該是說這比SVM好介紹...所以Adaboost先登場XD
不過, 通常Adaboost要登場前, 要先拿Bagging拿出來鞭
Bagging
一種ML演算法, 後來大多指sampling的方法, 這種演算法很簡單
我們手上有input, 我用一個classifier去學習他, 可是如果data太複雜怎辦?
所以乾脆這樣, 我用多個classifier來學這些data, 可是如果data都一樣, 那學完的結果還是一樣
所以呢, 乾脆取樣部份sample就好, 就用一招select with replacement來取樣
意思就是, 假設我有N筆data, 我取N筆, 但是每取一筆, 我就會放回, 最後得到的N', N' <= N
也就是可能會有重複的, 但是最後同一筆只算一次, 那數量就會比原本的N少
每個classifier所需要的data都做這種事情, 最後就會有T種classifier, 判斷也很簡單, 就叫這些classifier投票, 獲選可能的class最多的為主 (majority vote)
不過可惜的是,
Adaboost
最早由Yoav Freund 和 Robert Schapire一起在1996年提出(所以這是一個有17年以上的演算法....)
原文: http://www.face-rec.org/algorithms/Boosting-Ensemble/decision-theoretic_generalization.pdf
不想看原文沒關係, 由我來打打嘴泡XD (打完的感想...我根本自虐嘛!!!)
既然原名是Adaptive boosting, 就先從boosting開始講起
假設我今天有100筆資料要給電腦學習, 你手上需要寫一個演算法要去判斷這些資料, 所以去找了paper看ML演算法來判斷
結果因為厲害的演算法太複雜了或者是paper太難了看不懂, 只寫出了很笨很簡單的演算法(weak learner), 效果又不是那麼的好, 那怎麼辦呢?
那就用boosting吧!!, boosting可以加強你的笨笨演算法, 可以不停的演化修正錯誤達到高水準分類器!!
聽起來超威的耶, 那boosting要如何使出來呢? (絕對不是上上下下左左右右ABAB)
boosting的基本idea是這樣的, 你手上的演算法判斷了data之後, 每筆data都會有所謂的錯誤率, 透過修正這些錯誤率, 來強化原本的weak learner
也就是說, 假設每個training data都有個錯誤權重, 一開始大家都一樣, 因為還沒判斷, 等到weak learner開始判斷之後, 每個data都有自己的錯誤率, 把猜錯的提高權重, 猜對的降低權重, 如此一直循環下去, 就會慢慢的提昇learner的能力
PS1: 所以不能選太強的learner, 因為不容易加強
PS2: 所以learner要選可以餵入weight的
假設每個training data都有初始weight, D (distribution), 大家一開始都一樣, 當weak learner A學完第一輪之後, 判定大家的結果, 然後調整weight, 再用weak learner B去重新學調整過後的D, 然後weak learner C...etc
最後再統合(Ensemble)這些weak learner的結果, 來達到一個strong learner
那上述是簡易描述, 再來是眾多的定義
0. Weak learner, 稍微給點簡單定義, 以猜測正反來講, 隨機猜中的機率是0.5, 那weak learner大概就是比0.5再高的那麼一點點罷了, 這個內容會再另外交代
1. Input: 假設有N筆資料, x是feature的意思, y是所屬class, 通常paper會寫成 sequence of N labeled examples <(x1, y1), ..., (xN, yN)>, 那我們先著重在Binary的分類, 所以y基本上不是1 就是 -1 (是否之類的問題, 當然也可以是1 or 0, 到證明的時候會比較計較)
2. Iteration: 每次重新學習會是一個循環, 假設總共會重新學習 T 回, 每小回簡稱第t回
3. weight: 在這邊意思可以想成為distribution, 因為一開始大家都一樣, 所以一個簡單的預設初值可以這樣設定, D通常稱呼為 - distribution D over the N examples
t 就是上述的Iteration, D1的意思就是說第一回每個example的Distribution
4. 那再來就是用數學表示weak learner的結果, 首先每個learner 或者稱classifier, 都會學習一定的內容, 他會針對學習到的東西給一個假設, 例如說, 有一批人類的樣本學習, 然後他學到說假設眼睛有兩個以下的是人類, 這就是一個假設(hypothesis), 那來給點數學式
ht 意思就是第 t 回的weak learner, 那給定一個X vector, 會回傳1 or -1, X vector可以想成就是一筆眾多的features
5. error: 算錯誤率囉, 這應該很簡單, 把判斷錯的除以全部的數量, 就是錯誤率囉, trivial!!
6. 更新方法: 也就是前面說的, 有些權重要增加或減少, 更新的公式如下
至於那個α為甚麼會是那樣, 放到最後解釋
7. 合併: 那我們手上有了每個回合的weak learner, 要怎麼合併呢? 統統拿去做雞精!! 喔不是, 是統統加起來!!
取sign的意思就是, 大於0我就認為是1, 小於0我就認為是-1, that's all.
以偷懶的角度, 我可以說我已經解釋完整個Adaboost了...那這樣跟自己去看wiki根本沒差阿XDD
所以有些事情要交代一下, 那個α哪來的, 以及這樣的classifier真的有比較好嗎?
classifier好不好要看錯誤率, 錯誤率要能夠降的夠低才行
那想要降低錯誤率, 就要找出影響錯誤率的因子是哪些, 下面就會開始找出關鍵的因子!!
先來看一下distribution, 這邊有個比較tricky的部份, 為了推導方便, 需要把真實的class跟classifier的猜測做比較這件事情合併進入公式
如果猜對的話, 不管class是1 or -1, yi乘上ht(xi)都會是1, 反之, 都會是-1, 所以可以改寫為
也就是不對的時候負號會抵銷掉, 對的時候會留著, 跟原本的設定一樣
再來辛苦一點, 把他展開來觀察
好像沒什麼, 這時候做一件證明很常做的事情, 左邊全部乘起來, 右邊全部乘起來
當然在衝動把他寫下來之前, 會發現左右有項次可以互相消除, 消完之後整理就會變成
你會說, 奇怪, 替換了之後怎麼D1(i)怎麼不見了, 變成了1/N, 因為最一開始有假設, 第一回大家都是一樣的權重, 也就是1/N, 所以在這步我就順便替換了
再來稍微複雜一點點, 稍微來到Exponential的特性, Exponential的次方, 只要超過0, 都大於等於1
Exponential wiki: http://en.wikipedia.org/wiki/Exponential_function
那現在要來認真算錯誤率了, 假設, H(xi)犯錯的話, 會犯多少錯誤?
可以用數學表示大概會是怎樣的範圍嗎? 可以的, 但是要繞一點圈
假設H(xi)犯錯了, yi f(xi)會小於等於 0 (因為其中一個為1, 另外一個為-1), 那相乘的話一定小於0
所以配合exponential可以得到
我使用的工具不好打boolean operatior, 我改用indicator function表示, 也就是成立為1, 不成立為0
剛剛推完的Dt+1跟這邊好像很像, 我們把他合併來看一下
最後的步驟好像Dt+1不見了, 因為他是distribution, 最後全部加起來當然會是1, 所以一乘上去, 就消失囉
這裡告訴我們甚麼? 就是想要把錯誤率降低的話, 降低Zt 就可以了, 這邊可以想成是他的error upper bound
那這跟α甚麼關係呢? 其實事情是這樣的, 我上面只是找到了說, 如果今天會犯錯, 犯錯的錯誤率最大會被bound在Zt, 那所以只要想辦法把Zt弄小的話, 整個錯誤率就會下降對吧!!
那, 回到微積分, 所以只要我們對Zt做偏微 = 0, 就可以判斷出極值, 也就找到了可以下降的關鍵!! (並非所有演算法都可以這樣解, 只是這個剛好可以求出解來)
可以分出兩種狀況, 有猜對跟猜錯的, 所以可以改寫成下列結果
中間有把錯誤率ε替換一下, 意思就是, 我將可能分成兩種, 猜對跟猜錯, 然後替換一下
這邊過來那邊過去, 兩邊取ln, 就解出來了, 這就是α最美好的狀態, 可以讓錯誤率達到最低
基本上學到這邊該會的應該都會了, 剩餘的就是實做了!!
實做部分跟weak learner留到下一篇~!!
(以前我教授教我的Adaboost其實還有很多很難的東西, 大多是證明...但是我快忘光了XD, 等我想起來再補上, 這邊只是參考原作者的論文跟網路上比較常見的證明而已)
PS: 我用過而且算是好用的Adaboost tool有: 1. Weka 2.我教授他同窗的好友做的Lemga
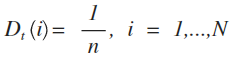













hi
回覆刪除你那個錯誤率是不是還要乘個權重啊