[ML] Classification & Regression Trees (CART)
上次提到了一個很簡單的 Decision Tree, 應該大多數人都可以很輕易理解
就字面上的含意, CART 會有兩種 Tree system, Classification Tree 以及 Regression Tree
所以他可以處理分類問題, 跟數字預測問題
Classification Tree
他的概念很簡單, 之前 Decision Tree 有可能是會切割出多個 branches
這次, 我們每次產生的 branch 只有 2 個, 也就是整顆 Tree 是個 Binary Tree
那 CART 跟 之前的 DT 最大的差異還有一點就是
原本 DT 是根據 information gain(IG) 來決定要怎麼切割
CART 是找個 impurity function(IF) 來決定要怎麼切割
那 IF 要解釋很費工夫, 簡單講就是判斷 data 純不純, 詳細內容有空的人可以先參考這篇
https://onlinecourses.science.psu.edu/stat557/node/85
那簡單講常見的 IF 有
根據 1. 錯誤率來切割 2. 用 Entropy (DT) 3. 用 Gini Index, 4. Towing
1. 錯誤率的意思是, 如果我某個切割方法完就判斷類別, 哪個切法錯誤率低我就選誰
而其實這問題會很多, 幾乎不會有人使用, 甚至會是怎麼切都沒有辦法更好
2. Entropy, 基本上因為用 Binary 切割下效果其實還好, 不算通用 (因為他效果比較好是在有multiple split 下的 Decision Tree)
3. Gini Index, CART 使用最廣泛的方法
舉個例子來說, 如果現在兩種 class: 0, 1, 共 800 筆 data
整個 data 的 impurity 則是 1 - (0.5)^2 - (0.5)^2 = 0.5
假設現在有一個 feature 有兩種 split 的方式, 兩種都可以變成 binary tree
這邊我列出可能的兩種切割結果, 在同一個 feature 下, 有 Xa 跟 Xb 的切法
Split Xa
假設切割在 Xa
左邊的 Child 會分到剩下 400 筆資料, class 0 的有 300筆, class 1 的有 100筆
左邊的 Child 計算 Gini Index 為: 1 - 0.752 - 0.252 = 0.375
右邊的 Child 會分到剩下 400 筆資料, class 0 的有 100筆, class 1 的有 300筆
右邊的 Child 計算 Gini Index 為: 1 - 0.252 - 0.752 = 0.375
因為左邊佔了 Total 的 0.5, 右邊也佔了 0.5, 所以這樣切割下來, 最後會得到
0.375 * 0.5 + 0.375 * 0.5 = 0.375
如下圖
Split Xb
假設切割在 Xb
左邊的 Child 會分到剩下 600筆資料, class 0 的有 400筆, class 1 的有 200筆
左邊的 Child 計算 Gini Index 為: 1 - 0.672 - 0.332 = 0.444
右邊的 Child 會分到剩下 200筆資料, class 0 的有 0筆, class 1 的有 200筆
右邊的 Child 計算 Gini Index 為: 1 - 02 - 12 = 0
因為左邊佔了 Total 的 0.75, 右邊佔了 0.25, 所以這樣切割下來, 最後會得到
0.444 * 0.75 + 0 * 0.25 = 0.333
如下圖
由此結果來判斷誰的貢獻最大, 也就是降低 Gini Index 最多的, 白話一點, 將純度降低較多者勝
那有些人可能不知道怎麼切 feature
簡單來說, 如果你 feature 是數字的
例如有一個 feature 是: 1, 1.2, 3.5, 4.7
你就可以在 <=1, <= 1.2, <= 3.5, <=4.7 之間做出 binary split
(數字當然可以增加更多選擇, 像是可以多做出一個都大於 4.7 的 split 也可以)
如果是 feature 是: 白, 黑, 黃
則更好處理, 可以針對是不是白, 是不是黑, 是不是黃, 做出 binary split
(要多一個都不是這些顏色的 split 也可以)
所以就不停的以這為條件, 一直的 split 下去, 直到剩下都一樣 class 為止
當然會overfit, 需要prune,
Pre-pruning
例如剩下的 instance 太少就停止, 或者是 impurity 數字降到多少就停止
但這作法有可能會容易造成 optimal 消失
Post-pruning
較常見的作法是, 先將 data 切成兩部份, 可能大約80% 20% 的比例
然後將80% 做類似 10 cross validation 的 training
也就是將剩下的 80% data, 做出10 組不同的 training data, 每個都差 10%
(ex: 第一組拿 80% 的後 90%, 第二組拿 80% 的前 10% 跟後 80%, 第三組前 20% 後 70%...etc)
也就是每組 training data 都是原先 data 的 72% 左右, 只是彼此之間都差了 10 %左右不一樣
(俗稱的 left one out)
然後利用這 10 組 data 建立出 10 顆 Tree
最後用最早切出來的 20% data 去 test 這 10 顆 Tree, 看誰結果好最後就用誰!!
下一篇沒意外應該是 Random Forest~
不過其實 Decision Tree 有相當多種變化, 這次來提一個也很常見的 Tree
Classification & Regression Trees (CART)
西元1984年, 由 Breiman, Friedman, Olshen, and Stone 等人發表的演算法
是一個比我還老的演算法....Orz
Breiman (1928 - 2005) 是個很強的教授, Random Forest (2001) 也是他發表的其中之一演算法
之後應該也會再寫個 Random Forest ~!!
Classification and Regression Tree
就字面上的含意, CART 會有兩種 Tree system, Classification Tree 以及 Regression Tree
所以他可以處理分類問題, 跟數字預測問題
Classification Tree
他的概念很簡單, 之前 Decision Tree 有可能是會切割出多個 branches
這次, 我們每次產生的 branch 只有 2 個, 也就是整顆 Tree 是個 Binary Tree
那 CART 跟 之前的 DT 最大的差異還有一點就是
原本 DT 是根據 information gain(IG) 來決定要怎麼切割
CART 是找個 impurity function(IF) 來決定要怎麼切割
那 IF 要解釋很費工夫, 簡單講就是判斷 data 純不純, 詳細內容有空的人可以先參考這篇
https://onlinecourses.science.psu.edu/stat557/node/85
那簡單講常見的 IF 有
根據 1. 錯誤率來切割 2. 用 Entropy (DT) 3. 用 Gini Index, 4. Towing
1. 錯誤率的意思是, 如果我某個切割方法完就判斷類別, 哪個切法錯誤率低我就選誰
而其實這問題會很多, 幾乎不會有人使用, 甚至會是怎麼切都沒有辦法更好
2. Entropy, 基本上因為用 Binary 切割下效果其實還好, 不算通用 (因為他效果比較好是在有multiple split 下的 Decision Tree)
3. Gini Index, CART 使用最廣泛的方法
舉個例子來說, 如果現在兩種 class: 0, 1, 共 800 筆 data
整個 data 的 impurity 則是 1 - (0.5)^2 - (0.5)^2 = 0.5
假設現在有一個 feature 有兩種 split 的方式, 兩種都可以變成 binary tree
這邊我列出可能的兩種切割結果, 在同一個 feature 下, 有 Xa 跟 Xb 的切法
Split Xa
| split on Xa | Left Child | Right Child | ||
|---|---|---|---|---|
| Class | 0:300 | 1:100 | 0:100 | 1:300 |
| Gini Index | 0.375 | 0.375 | ||
| Total Contrib. | 0.375 | |||
假設切割在 Xa
左邊的 Child 會分到剩下 400 筆資料, class 0 的有 300筆, class 1 的有 100筆
左邊的 Child 計算 Gini Index 為: 1 - 0.752 - 0.252 = 0.375
右邊的 Child 會分到剩下 400 筆資料, class 0 的有 100筆, class 1 的有 300筆
右邊的 Child 計算 Gini Index 為: 1 - 0.252 - 0.752 = 0.375
因為左邊佔了 Total 的 0.5, 右邊也佔了 0.5, 所以這樣切割下來, 最後會得到
0.375 * 0.5 + 0.375 * 0.5 = 0.375
如下圖
Split Xb
| split on Xb | Left Child | Right Child | ||
|---|---|---|---|---|
| Class | 0:400 | 1:200 | 0:0 | 1:200 |
| Gini Index | 0.444 | 0 | ||
| Total Contrib. | 0.333 | |||
假設切割在 Xb
左邊的 Child 會分到剩下 600筆資料, class 0 的有 400筆, class 1 的有 200筆
左邊的 Child 計算 Gini Index 為: 1 - 0.672 - 0.332 = 0.444
右邊的 Child 會分到剩下 200筆資料, class 0 的有 0筆, class 1 的有 200筆
右邊的 Child 計算 Gini Index 為: 1 - 02 - 12 = 0
因為左邊佔了 Total 的 0.75, 右邊佔了 0.25, 所以這樣切割下來, 最後會得到
0.444 * 0.75 + 0 * 0.25 = 0.333
如下圖
由此結果來判斷誰的貢獻最大, 也就是降低 Gini Index 最多的, 白話一點, 將純度降低較多者勝
Regression Tree
regression 這邊的狀況其實類似, 但是他是針對 regression problem (預測數字)
也就是說, 上述的 classification tree 最後在 leaf 的是 class, 但是這邊最後在 leaf 的會是 number
regression tree 一樣是切割之後, 需要利用一些 function 來幫你判斷 data 經過切割後的變化
這邊靠的是 minimize square error, 也就是選定一個切割條件
然後一樣會分成左右兩個 child, 但這邊 data 沒有 class 了, 但是有各別的 value (答案)
他要計算的就是你分割出來的左右兩個 child, 各依照上面剩下的 data 去計算跟答案的平方差距
選差距最小的, 就是我要切割的 feature 為 node (也就是說, 分割出來的那些 data 的答案都差不多接近)
那有些人可能不知道怎麼切 feature
簡單來說, 如果你 feature 是數字的
例如有一個 feature 是: 1, 1.2, 3.5, 4.7
你就可以在 <=1, <= 1.2, <= 3.5, <=4.7 之間做出 binary split
(數字當然可以增加更多選擇, 像是可以多做出一個都大於 4.7 的 split 也可以)
如果是 feature 是: 白, 黑, 黃
則更好處理, 可以針對是不是白, 是不是黑, 是不是黃, 做出 binary split
(要多一個都不是這些顏色的 split 也可以)
所以就不停的以這為條件, 一直的 split 下去, 直到剩下都一樣 class 為止
當然會overfit, 需要prune,
Pre-pruning
例如剩下的 instance 太少就停止, 或者是 impurity 數字降到多少就停止
但這作法有可能會容易造成 optimal 消失
Post-pruning
較常見的作法是, 先將 data 切成兩部份, 可能大約80% 20% 的比例
然後將80% 做類似 10 cross validation 的 training
也就是將剩下的 80% data, 做出10 組不同的 training data, 每個都差 10%
(ex: 第一組拿 80% 的後 90%, 第二組拿 80% 的前 10% 跟後 80%, 第三組前 20% 後 70%...etc)
也就是每組 training data 都是原先 data 的 72% 左右, 只是彼此之間都差了 10 %左右不一樣
(俗稱的 left one out)
然後利用這 10 組 data 建立出 10 顆 Tree
最後用最早切出來的 20% data 去 test 這 10 顆 Tree, 看誰結果好最後就用誰!!
下一篇沒意外應該是 Random Forest~
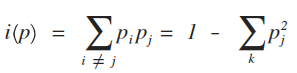


引用
回覆刪除"由此結果來判斷誰的貢獻最大, 也就是降低 Gini Index 最多的, 白話一點, 將純度降低較多者勝"
請問大大
降低Gini index的量多, 不是指將純度提高嗎?
我想應該是筆誤吧,應該是純度較高比較好。
刪除Gini impurity (index) 指的是資料不純度的指標。
因此 Gini impurity 降低代表,資料的純度提高是沒有錯的。