[ML] Decision Tree (revision 3)
來提個我工作上我還滿喜歡使用的演算法 - Decision Tree
decision tree 基本上 google 一下應該就可以找到很多東西
不過要注意的是要 google 的是 decision tree learning
之前在講 Adaboost 有稍微提到這東西, Decision Stump 就是一個簡化版的 Decision Tree
這東西其實說起來相當簡單, 嗯, 其實做起來也超級簡單XD
簡單提一下, 這邊有一個很有趣的網站 - http://en.akinator.com/
遊戲是這樣的, 你可以心中想一個人, 然後回答他的問題, 他問題答案只會是 - 是/否
回答他的問題一定的量之後, 他就會猜你心中想的人物
那, 這背後當然是有龐大的資料庫跟使用者回饋
不過技術上, 就很像是Decision Tree
題外話: 我還真的有去買C4.5作者的書, 可是有一半內容就只是把C4.5的程式碼印上去...
C4.5 是一個很有名的 Decision Tree algorithm, 新版本叫做C5.0
故事是這樣的
假設你今天要出去玩, 你可能會跟據天氣, 溫度, 濕度...etc
來決定你最後是否要出去玩
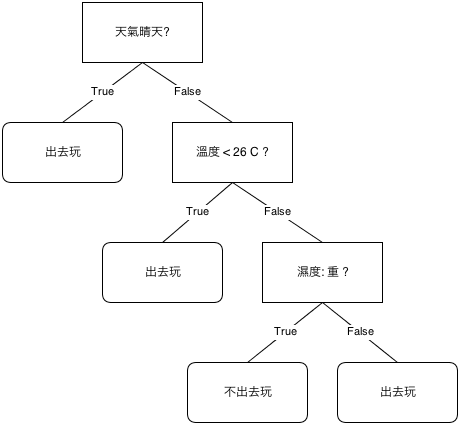
那舉例來說, 1. 天氣: 晴天 -> 出去玩, 結案
2. 天氣: 非晴天, 溫度 < 26 C ? -> 出去玩, 結案
3. 天氣: 非晴天, 溫度 > 26, 濕度: 重 -> 不出去玩, 結案
4. 天氣: 非晴天, 溫度 > 26, 濕度: 不重 -> 出去玩, 結案
眾多的決策合起來, 就是個 Decision Tree, 如下圖
Decision Tree 是一個非常常見的分類演算法 (Classification Algorithm)
從上述案例應該就差不多有點感覺了, 那來討論一下要如何建立這樣的一顆 Tree
首先可能會有人困惑, 為甚麼要從天氣開始? 為啥不從溫度開始?
其實這是有一些 Information Theory 在背後支持的
要建立這樣的一顆 Tree, 要先有第一個node
當然就是要先從 training data 中, 挑個 feature 出來
首先, 我們先用笨一點的方法, 假設我們手上有 10 個 feature, 我就一個一個試
假設第一回從第一個 feature 決定 -> 然後就只靠這個 feature 判斷結論
然後第二回, 從第二個 feature 決定 ...etc
一直 run 完 10 回, 然後看這十個 feature, 哪個結果最好, 就先從他開始切割
建立好第一個 node 之後, 就會切成左右兩種, 剛好等於把 data 切割成兩種 branches
然後再繼續用同樣的方式, 一個一個試, 看要在哪個 feature 切割的結果會比較好 (data 已經少一些了)
就這樣一直下去到剩餘的條件都一樣, 而且類別也都一樣, 那就可以結束這個 branch 了
這邊一樣是說得很簡單, 但有個細節還需要多一點討論, 例如怎樣叫好?
先來提一下兩個很有趣的terminology - Entropy & Information Gain
entropy wiki: http://en.wikipedia.org/wiki/Information_entropy
information gain wiki: http://en.wikipedia.org/wiki/Information_gain_in_decision_trees
Entropy formula
Information Gain formula
Entropy 是 Shannon 當初從熱力學導入到資訊理論的, 所以也稱為: Shannon entropy
這東西其實滿抽象的, 簡單講他是一種去衡量不確定性(亂)的公式, 數字越高不確定性越高
例如, 我要衡量投擲硬幣的不確定性, 硬幣只會有 正 / 反 (Head / Tail)
如果這是一枚公正的硬幣, 那機率各是 0.5 / 0.5,
則根據公式 (log 以 2 為底)
我們可以得到: - (0.5 * log(0.5) + 0.5 * log(0.5)) = 1 (不明確, 不確定性高)
如果今天是不公正的硬幣, 機率是 1 / 0 (兩面都是 Head)
則我們可以得到: - (1 * log(1) + 0 * log(0)) = 0, (可以明確預測, 不確定性低)
不明確性低就表示我可以很容易就猜到結果
這邊再給予網路上另一範例用 data 說明 (下方會有詳細範例)
Sample這邊稱為S, S(9+, 5-) 意思為Sample有14筆, 9個class為+, 5個class為-
則H(S) = -(9/14) * log(9/14) - (5/14)*log(5/14) = 0.940
9/14 正數占全體的比例, 5/14為負數占全體的比例
簡單講, 這是再講如何計算 data 的亂度, 像上面舉例的 data, 就滿亂的, 所以不明確高
那, 我要如何使用這個東西來做 Decision Tree ?
假設整個 dataset 的亂度是0.940, 如果我今天切割在某個 feature α, 將這個 dataset 切成了兩部份
結果讓整個 dataset 的亂度下降到了 0.5, 則 0.94 - 0.5 就是 切割在 α 的Information Gain
也就是說, 你因為切在 feature α 導致這個dataset的亂度下降到0.5(難易度下降)
這是好事情, 因為下降了, 所以此 dataset 變得更容易處理的
根據上面的流程, 切割在哪一點的演算法就出來了
首先要先算出整體的 entropy, 然後每個 feature都要去計算他相對應的 information gain
能夠得到最多的 information gain (也就是可以降低 dataset 亂度最多的) 就是切割點
所以依照找 information gain 找 feature 當 node, 然後切割, 然後找 feature, 切割
一直循序下去到每個 branch 最後剩下的 dataset 都是同一種class, 也就是走到了 leaf
就完成了 Decision Tree !!
舉個教科書上最常見的例子, 假設現在有 14 筆 data
總共有四種 feature, outlook, temperature, humidity, windy 跟 binary class - play (yes/no)
那拿到資料第一件要做的事情是, 先看整個資料亂不亂 !!
根據play 重新整理一下整個 data
假設 data 我們稱呼為 S, 要算的是在乎 play 的前提下的亂度 (9+, 5-)
我們發現, 滿亂的!!
所以我們要進行切割, 要想辦法找一個可以讓資料庫"整齊"一點的切割
我們有四個選擇 feature, outlook, temperature, humidity and windy
就要分別計算切割在這四種 feature 上的 Entropy, 然後計算是相對應的Information Gain
所以要計算H(outlook), H(temperature), H(humidity), H(windy)
首先先來計算outlook 上的 Entropy
那要注意的事情是, 若是在 outlook 上切割, 將會把資料分成三部份
所以在記算 IG 的時候, 也要將相對造成的 Entropy 乘上所佔的資料百分比
那相對於其他的 feature 也都可以依此算出相對的 Information Gain
所以看到這些 Information Gain 之後, 就可以判斷出從誰分割出來, 就可以讓資料不那麼亂
也就是從 outlook 出發, 是最好的選擇 !!
後續就是將資料分割成三種類型, sunny, overcast, rainy
然後先檢驗是否剩下的 data 的 class 都一樣
如果不一樣, 就可以繼續造上述的方式繼續找feature 做切割, 一直做到都一樣 class 為止
那碰到Numerical 找尋切割點怎麼辦?
假設 dataset 的某個 feature 依序排列有: 1:24, 1:25, 1:27, 1:29, 那我們要找的就是在 v < 24, 24 < v < 25, 25 < v < 27, 27 < v < 29, 29 < v 這幾個區間找尋, 也就是將此feature 看待成有五種類型來計算他的 Information gain & entropy
當然其實也有其他 paper在討論 numerical 的其他處理方式
最後Decision Tree 會是從一開始有一個 Node - feature, 一堆 Node - 一直延伸到 Leaf - class
所以 predict 也相對的簡單, 當 input data 依照 Node 順序走, 走到最後就是猜測的 class
這篇講的那麼簡單其實是為了未來了 Random Forest 鋪梗XD (不過好像還要講CART才行...orz)
這個 Decision Tree 也可以稱呼為 ID3 Algorithm : http://en.wikipedia.org/wiki/ID3_algorithm
那, 有時候, 為了怕這個過程會讓整棵 Tree 長的太過深遠, 而導致 Overfitting
所以通常會做一些 prune, 作法很單純, 當 Tree 建完了之後, 開始從 leaf 往回推
假設我不要做到100 % 分割率, 我只要有90 %就好
我就有可能會把某個 node以下的 leaf 合併上來, 也就是修剪一些可能分類過頭的 branch
那要注意的是, 如果碰到像是日期或是序號這種 feature
要小心不要用 Information Gain 或者不應該採納類似的 feature
因為切割在每個序號 (因為不重複大家都不一樣)
會得到超大的 Information Gain, 你會得到的是, 只要切割在序號上, 你就會超不亂
聽起來很好阿, 資料庫變簡單了, 但是這是個悲劇, 因為你會建立出一個超寬的 Tree
一個 feature 然後切割出幾乎跟 training data 一樣多的 branches, 完全悲劇
稱呼他為悲劇的原因是, test data 理應序號也都不一樣, 透過序號這個 feature 去判斷
會完全沒辦法判斷出合理的結果
所以也有人會使用 Gain Ratio (C4.5) 來判斷, 用Gini Index (CART) 來判斷
decision tree 基本上 google 一下應該就可以找到很多東西
不過要注意的是要 google 的是 decision tree learning
之前在講 Adaboost 有稍微提到這東西, Decision Stump 就是一個簡化版的 Decision Tree
這東西其實說起來相當簡單, 嗯, 其實做起來也超級簡單XD
簡單提一下, 這邊有一個很有趣的網站 - http://en.akinator.com/
遊戲是這樣的, 你可以心中想一個人, 然後回答他的問題, 他問題答案只會是 - 是/否
回答他的問題一定的量之後, 他就會猜你心中想的人物
那, 這背後當然是有龐大的資料庫跟使用者回饋
不過技術上, 就很像是Decision Tree
題外話: 我還真的有去買C4.5作者的書, 可是有一半內容就只是把C4.5的程式碼印上去...
C4.5 是一個很有名的 Decision Tree algorithm, 新版本叫做C5.0
Decision Tree
故事是這樣的
假設你今天要出去玩, 你可能會跟據天氣, 溫度, 濕度...etc
來決定你最後是否要出去玩
那舉例來說, 1. 天氣: 晴天 -> 出去玩, 結案
2. 天氣: 非晴天, 溫度 < 26 C ? -> 出去玩, 結案
3. 天氣: 非晴天, 溫度 > 26, 濕度: 重 -> 不出去玩, 結案
4. 天氣: 非晴天, 溫度 > 26, 濕度: 不重 -> 出去玩, 結案
眾多的決策合起來, 就是個 Decision Tree, 如下圖
Decision Tree 是一個非常常見的分類演算法 (Classification Algorithm)
從上述案例應該就差不多有點感覺了, 那來討論一下要如何建立這樣的一顆 Tree
首先可能會有人困惑, 為甚麼要從天氣開始? 為啥不從溫度開始?
其實這是有一些 Information Theory 在背後支持的
要建立這樣的一顆 Tree, 要先有第一個node
當然就是要先從 training data 中, 挑個 feature 出來
首先, 我們先用笨一點的方法, 假設我們手上有 10 個 feature, 我就一個一個試
假設第一回從第一個 feature 決定 -> 然後就只靠這個 feature 判斷結論
然後第二回, 從第二個 feature 決定 ...etc
一直 run 完 10 回, 然後看這十個 feature, 哪個結果最好, 就先從他開始切割
建立好第一個 node 之後, 就會切成左右兩種, 剛好等於把 data 切割成兩種 branches
然後再繼續用同樣的方式, 一個一個試, 看要在哪個 feature 切割的結果會比較好 (data 已經少一些了)
就這樣一直下去到剩餘的條件都一樣, 而且類別也都一樣, 那就可以結束這個 branch 了
這邊一樣是說得很簡單, 但有個細節還需要多一點討論, 例如怎樣叫好?
先來提一下兩個很有趣的terminology - Entropy & Information Gain
Entropy & Information Gain
entropy wiki: http://en.wikipedia.org/wiki/Information_entropy
information gain wiki: http://en.wikipedia.org/wiki/Information_gain_in_decision_trees
Entropy formula
Information Gain formula
Entropy 是 Shannon 當初從熱力學導入到資訊理論的, 所以也稱為: Shannon entropy
這東西其實滿抽象的, 簡單講他是一種去衡量不確定性(亂)的公式, 數字越高不確定性越高
例如, 我要衡量投擲硬幣的不確定性, 硬幣只會有 正 / 反 (Head / Tail)
如果這是一枚公正的硬幣, 那機率各是 0.5 / 0.5,
則根據公式 (log 以 2 為底)
我們可以得到: - (0.5 * log(0.5) + 0.5 * log(0.5)) = 1 (不明確, 不確定性高)
如果今天是不公正的硬幣, 機率是 1 / 0 (兩面都是 Head)
則我們可以得到: - (1 * log(1) + 0 * log(0)) = 0, (可以明確預測, 不確定性低)
不明確性低就表示我可以很容易就猜到結果
這邊再給予網路上另一範例用 data 說明 (下方會有詳細範例)
Sample這邊稱為S, S(9+, 5-) 意思為Sample有14筆, 9個class為+, 5個class為-
則H(S) = -(9/14) * log(9/14) - (5/14)*log(5/14) = 0.940
9/14 正數占全體的比例, 5/14為負數占全體的比例
簡單講, 這是再講如何計算 data 的亂度, 像上面舉例的 data, 就滿亂的, 所以不明確高
那, 我要如何使用這個東西來做 Decision Tree ?
假設整個 dataset 的亂度是0.940, 如果我今天切割在某個 feature α, 將這個 dataset 切成了兩部份
結果讓整個 dataset 的亂度下降到了 0.5, 則 0.94 - 0.5 就是 切割在 α 的Information Gain
也就是說, 你因為切在 feature α 導致這個dataset的亂度下降到0.5(難易度下降)
這是好事情, 因為下降了, 所以此 dataset 變得更容易處理的
根據上面的流程, 切割在哪一點的演算法就出來了
首先要先算出整體的 entropy, 然後每個 feature都要去計算他相對應的 information gain
能夠得到最多的 information gain (也就是可以降低 dataset 亂度最多的) 就是切割點
所以依照找 information gain 找 feature 當 node, 然後切割, 然後找 feature, 切割
一直循序下去到每個 branch 最後剩下的 dataset 都是同一種class, 也就是走到了 leaf
就完成了 Decision Tree !!
舉個教科書上最常見的例子, 假設現在有 14 筆 data
總共有四種 feature, outlook, temperature, humidity, windy 跟 binary class - play (yes/no)
| outlook | temperature | humidity | windy | play |
|---|---|---|---|---|
| sunny | hot | high | FALSE | no |
| sunny | hot | high | TRUE | no |
| overcast | hot | high | FALSE | yes |
| rainy | mild | high | FALSE | yes |
| rainy | cool | normal | FALSE | yes |
| rainy | cool | normal | TRUE | no |
| overcast | cool | normal | TRUE | yes |
| sunny | mild | high | FALSE | no |
| sunny | cool | normal | FALSE | yes |
| rainy | mild | normal | FALSE | yes |
| sunny | mild | normal | TRUE | yes |
| overcast | mild | high | TRUE | yes |
| overcast | hot | normal | FALSE | yes |
| rainy | mild | high | TRUE | no |
那拿到資料第一件要做的事情是, 先看整個資料亂不亂 !!
根據play 重新整理一下整個 data
| outlook | temperature | humidity | windy | play | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| yes | no | yes | no | yes | no | yes | no | yes | no | ||||
| sunny | 2 | 3 | hot | 2 | 2 | high | 3 | 4 | FALSE | 6 | 2 | 9 | 5 |
| overcast | 4 | 0 | mild | 4 | 2 | normal | 6 | 1 | TRUE | 3 | 3 | ||
| rainy | 3 | 2 | cool | 3 | 1 | ||||||||
假設 data 我們稱呼為 S, 要算的是在乎 play 的前提下的亂度 (9+, 5-)
我們發現, 滿亂的!!
所以我們要進行切割, 要想辦法找一個可以讓資料庫"整齊"一點的切割
我們有四個選擇 feature, outlook, temperature, humidity and windy
就要分別計算切割在這四種 feature 上的 Entropy, 然後計算是相對應的Information Gain
所以要計算H(outlook), H(temperature), H(humidity), H(windy)
首先先來計算outlook 上的 Entropy
那要注意的事情是, 若是在 outlook 上切割, 將會把資料分成三部份
所以在記算 IG 的時候, 也要將相對造成的 Entropy 乘上所佔的資料百分比
那相對於其他的 feature 也都可以依此算出相對的 Information Gain
所以看到這些 Information Gain 之後, 就可以判斷出從誰分割出來, 就可以讓資料不那麼亂
也就是從 outlook 出發, 是最好的選擇 !!
後續就是將資料分割成三種類型, sunny, overcast, rainy
然後先檢驗是否剩下的 data 的 class 都一樣
如果不一樣, 就可以繼續造上述的方式繼續找feature 做切割, 一直做到都一樣 class 為止
那碰到Numerical 找尋切割點怎麼辦?
假設 dataset 的某個 feature 依序排列有: 1:24, 1:25, 1:27, 1:29, 那我們要找的就是在 v < 24, 24 < v < 25, 25 < v < 27, 27 < v < 29, 29 < v 這幾個區間找尋, 也就是將此feature 看待成有五種類型來計算他的 Information gain & entropy
當然其實也有其他 paper在討論 numerical 的其他處理方式
最後Decision Tree 會是從一開始有一個 Node - feature, 一堆 Node - 一直延伸到 Leaf - class
所以 predict 也相對的簡單, 當 input data 依照 Node 順序走, 走到最後就是猜測的 class
這篇講的那麼簡單其實是為了未來了 Random Forest 鋪梗XD (不過好像還要講CART才行...orz)
這個 Decision Tree 也可以稱呼為 ID3 Algorithm : http://en.wikipedia.org/wiki/ID3_algorithm
那, 有時候, 為了怕這個過程會讓整棵 Tree 長的太過深遠, 而導致 Overfitting
所以通常會做一些 prune, 作法很單純, 當 Tree 建完了之後, 開始從 leaf 往回推
假設我不要做到100 % 分割率, 我只要有90 %就好
我就有可能會把某個 node以下的 leaf 合併上來, 也就是修剪一些可能分類過頭的 branch
那要注意的是, 如果碰到像是日期或是序號這種 feature
要小心不要用 Information Gain 或者不應該採納類似的 feature
因為切割在每個序號 (因為不重複大家都不一樣)
會得到超大的 Information Gain, 你會得到的是, 只要切割在序號上, 你就會超不亂
聽起來很好阿, 資料庫變簡單了, 但是這是個悲劇, 因為你會建立出一個超寬的 Tree
一個 feature 然後切割出幾乎跟 training data 一樣多的 branches, 完全悲劇
稱呼他為悲劇的原因是, test data 理應序號也都不一樣, 透過序號這個 feature 去判斷
會完全沒辦法判斷出合理的結果
所以也有人會使用 Gain Ratio (C4.5) 來判斷, 用Gini Index (CART) 來判斷








最後四個方程式應該加減號有錯~
回覆刪除應該都是減號吧!?
謝謝指教
阿對!!! 感激指正, 我忘記加上括號了, 已經修改好了 ~ 感謝 ^^
刪除講得清楚明瞭,讚!
回覆刪除您的解說是我看過最清楚明瞭的,太讚了!!!
回覆刪除請問為啥切割不是temperature而是outlook 0.029不是比較小嗎?
回覆刪除從可以獲得最多的 Information gain 開始切割, 理論上效果會最好, 越小表示從那邊切割後續獲得的資訊量也越小, 而 outlook 是當下算起來最多的
刪除謝謝 原來我把亂度和IG搞混了
刪除